我对动态规划的理解

动态规划

动态规划的思考

首先，算法一般是可以用枚举来发现规律的，不是100%，因为有些问题的计算，是可以通过数学公式反而直接算出来了

算法都是一个过程，从规模从小到大发现规律或者从规模大到小发现规律

• 递推问题规律

  • 从规模小的问题到规模大的问题，规模大的问题依赖仅仅规模小的问题的结果，那么这样可以避免重复计算小规模的问题。比如求一个等差数列的和，这种问题，就是仅仅依赖了前一个子问题的结果
    比如，1，2，3，4，… 这个数列如果不用公式计算，就是不断累加前一次的结果。
  • 规模大的问题，依赖多个小规模的问题的结果，这种情况下就很可能存在重复计算，为什么呢？
    比如斐波那契数列，如f(n) = f(n-1) + f(n-2) -> f(n) = (f(n-2) + f(n-3)) + f(n-2)，如果f(n-2)这个函数没有计算缓存的话，那么就会导致重复计算。有解决办法吗？有，存储已经计算过的值，如果当前这个规模问题已经计算过就立即返回结果，备忘录模式

• 路径问题规律

  • 比如路径问题，寻找从A点到B点，有多少条路径。因为目标比较明确，从感觉上来看，这个问题和规模B点的问题相关性最大，所以如果从A点作为思考，这会出现一个问题，有些情况下需要考虑回溯。
    如下图：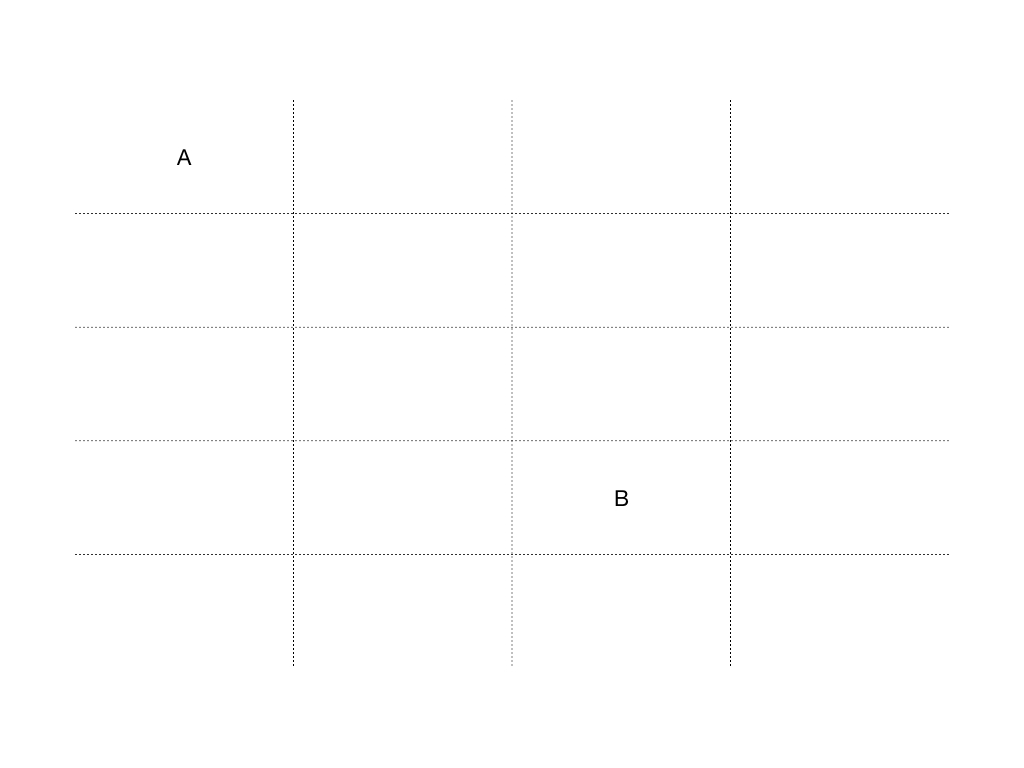
    

    1. 如果上面是A到B的移动过程中，只能往左边或者右边移动的时候。A可能存在直接走到最右则，而无法到达B，因为题设条件限制。所以这时从A思考，会产生回溯，当某一步不能达到目标的时候，要回退上一次的计算，并且选择另外一个路径执行（基于计算另外一个能够达到目标的子问题）。所以，就产生了不确定性，需要回溯，可以根据B的X和Y坐标，控制边界，减少不必要的回溯。

    2. 如果上面的问题是从目的地思考，反推上一步的来源。那么这个问题就清晰了。由于题设限制只能往右边或者下边移动，所以到达B点时，肯定是从左边或者从上边的格子过来的。这样问题就清晰了，到达B点，从B的左边格子过来+从B的上边格子过来这两种情况，通过枚举情形，问题是确定的，而且这些计算不用回溯，控制好逆向的路径，不越过A的X和Y坐标就好了。直到接近A点。不过，当前这种从规模高到低的问题，存在重复计算的问题，需要设置计算缓存（备忘录模式）

如果从上方考到思考过程，我们可以枚举一下情形，从小规模到大规模，或者从大规模到小规模来寻找思路。

状态转移方程–待续

最优子结构–待续

边界–待续